Logic Gates Cheat Sheet removed at m4yh3m's request until an updated version is made available. Joined Apr 28, 2004 186. Administration Calculation Logic Generic Logic: 14: Matrix Logic: PL, PG: To provide values for second dimension of a Price List. Administration Calculation Logic Generic Logic: api.product('sku') A visible element must return a list of strings. 15: PriceAnalyzer Logic: DF, DS, DM: Administration Calculation Logic PriceAnalyzer. Find your keyboard shortcut cheat sheets here: Please choose your cheat sheet beneath: Ableton Live 10. Logic Pro X: Maya 2019: Media Composer 9: Photoshop CC.
By Afshine Amidi and Shervine Amidi
Basics
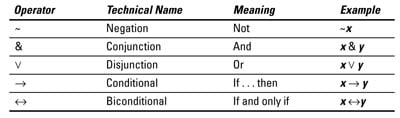
Syntax of propositional logic By noting $f,g$ formulas, and $neg, wedge, vee, rightarrow, leftrightarrow$ connectives, we can write the following logical expressions:
| Name | Symbol | Meaning | Illustration |
| Affirmation | $f$ | $f$ | |
| Negation | $neg f$ | not $f$ | |
| Conjunction | $fwedge g$ | $f$ and $g$ | |
| Disjunction | $fvee g$ | $f$ or $g$ | |
| Implication | $frightarrow g$ | if $f$ then $g$ | |
| Biconditional | $fleftrightarrow g$ | $f$, that is to say $g$ |
Remark: formulas can be built up recursively out of these connectives.
Model A model $w$ denotes an assignment of binary weights to propositional symbols.
Example: the set of truth values $w = {A:0, B:1, C:0}$ is one possible model to the propositional symbols $A$, $B$ and $C$.
Interpretation function The interpretation function $mathcal{I}(f,w)$ outputs whether model $w$ satisfies formula $f$:
Set of models $mathcal{M}(f)$ denotes the set of models $w$ that satisfy formula $f$. Mathematically speaking, we define it as follows:
Knowledge base
Definition The knowledge base $textrm{KB}$ is the conjunction of all formulas that have been considered so far. The set of models of the knowledge base is the intersection of the set of models that satisfy each formula. In other words:
Probabilistic interpretation The probability that query $f$ is evaluated to $1$ can be seen as the proportion of models $w$ of the knowledge base $textrm{KB}$ that satisfy $f$, i.e.:
Satisfiability The knowledge base $textrm{KB}$ is said to be satisfiable if at least one model $w$ satisfies all its constraints. In other words:
Remark: $mathcal{M}(textrm{KB})$ denotes the set of models compatible with all the constraints of the knowledge base.
Relation between formulas and knowledge base We define the following properties between the knowledge base $textrm{KB}$ and a new formula $f$:
| Name | Mathematical formulation | Illustration | Notes |
| $textrm{KB}$ entails $f$ | $mathcal{M}(textrm{KB})capmathcal{M}(f)=mathcal{M}(textrm{KB})$ | • $f$ does not bring any new information • Also written $textrm{KB}models f$ | |
| $textrm{KB}$ contradicts $f$ | $mathcal{M}(textrm{KB})capmathcal{M}(f)=varnothing$ | • No model satisfies the constraints after adding $f$ • Equivalent to $textrm{KB}modelsneg f$ | |
| $f$ contingent to $textrm{KB}$ | $mathcal{M}(textrm{KB})capmathcal{M}(f) neq varnothing$ and $mathcal{M}(textrm{KB})capmathcal{M}(f)neqmathcal{M}(textrm{KB})$ | • $f$ does not contradict $textrm{KB}$ • $f$ adds a non-trivial amount of information to $textrm{KB}$ |
Model checking A model checking algorithm takes as input a knowledge base $textrm{KB}$ and outputs whether it is satisfiable or not.
Remark: popular model checking algorithms include DPLL and WalkSat.
Inference rule An inference rule of premises $f_1,...,f_k$ and conclusion $g$ is written:
Forward inference algorithm From a set of inference rules $textrm{Rules}$, this algorithm goes through all possible $f_1, ..., f_k$ and adds $g$ to the knowledge base $textrm{KB}$ if a matching rule exists. This process is repeated until no more additions can be made to $textrm{KB}$.
Derivation We say that $textrm{KB}$ derives $f$ (written $textrm{KB}vdash f$) with rules $textrm{Rules}$ if $f$ already is in $textrm{KB}$ or gets added during the forward inference algorithm using the set of rules $textrm{Rules}$.
Properties of inference rules A set of inference rules $textrm{Rules}$ can have the following properties:
| Name | Mathematical formulation | Notes |
| Soundness | ${f , | , textrm{KB}vdash f}subseteq{f , | , textrm{KB}models f}$ | • Inferred formulas are entailed by $textrm{KB}$ • Can be checked one rule at a time • 'Nothing but the truth' |
| Completeness | ${f , | , textrm{KB}vdash f}supseteq{f , | , textrm{KB}models f}$ | • Formulas entailing $textrm{KB}$ are either already in the knowledge base or inferred from it • 'The whole truth' |
Propositional logic
In this section, we will go through logic-based models that use logical formulas and inference rules. The idea here is to balance expressivity and computational efficiency.
Horn clause By noting $p_1,...,p_k$ and $q$ propositional symbols, a Horn clause has the form:
Remark: when $q=textrm{false}$, it is called a 'goal clause', otherwise we denote it as a 'definite clause'.
Modus ponens For propositional symbols $f_1,...,f_k$ and $p$, the modus ponens rule is written:
Remark: it takes linear time to apply this rule, as each application generate a clause that contains a single propositional symbol.
Completeness Modus ponens is complete with respect to Horn clauses if we suppose that $textrm{KB}$ contains only Horn clauses and $p$ is an entailed propositional symbol. Applying modus ponens will then derive $p$.
Conjunctive normal form A conjunctive normal form (CNF) formula is a conjunction of clauses, where each clause is a disjunction of atomic formulas.
Remark: in other words, CNFs are $wedge$ of $vee$.



Equivalent representation Every formula in propositional logic can be written into an equivalent CNF formula. The table below presents general conversion properties:
| Rule name | Initial | Converted | |
| Eliminate | $leftrightarrow$ | $f leftrightarrow g$ | $(f rightarrow g) wedge (g rightarrow f)$ |
| $rightarrow$ | $f rightarrow g$ | $neg f vee g$ | |
| $negneg$ | $negneg f$ | $f$ | |
| Distribute | $neg$ over $wedge$ | $neg(f wedge g)$ | $neg f vee neg g$ |
| $neg$ over $vee$ | $neg(f vee g)$ | $neg fwedge neg g$ | |
| $vee$ over $wedge$ | $f vee (g wedge h)$ | $(f vee g) wedge (f vee h)$ | |
Resolution rule For propositional symbols $f_1,...,f_n$, and $g_1,...,g_m$ as well as $p$, the resolution rule is written:
Remark: it can take exponential time to apply this rule, as each application generates a clause that has a subset of the propositional symbols.
Resolution-based inference The resolution-based inference algorithm follows the following steps:
- Step 1: Convert all formulas into CNF
- Step 2: Repeatedly apply resolution rule
- Step 3: Return unsatisfiable if and only if $text{False}$ is derived
First-order logic
The idea here is to use variables to yield more compact knowledge representations.
Model A model $w$ in first-order logic maps:
- constant symbols to objects
- predicate symbols to tuple of objects
Horn clause By noting $x_1,...,x_n$ variables and $a_1,...,a_k,b$ atomic formulas, the first-order logic version of a horn clause has the form:
Formal Logic Cheat Sheet
Substitution A substitution $theta$ maps variables to terms and $textrm{Subst}[theta,f]$ denotes the result of substitution $theta$ on $f$.
Unification Unification takes two formulas $f$ and $g$ and returns the most general substitution $theta$ that makes them equal:
Note: $textrm{Unify}[f,g]$ returns $textrm{Fail}$ if no such $theta$ exists.
Modus ponens By noting $x_1,...,x_n$ variables, $a_1, ..., a_k$ and $a'_1,...,a'_k$ atomic formulas and by calling $theta = textrm{Unify}(a'_1wedge ...wedge a'_k, a_1wedge ...wedge a_k)$, the first-order logic version of modus ponens can be written:
Completeness Modus ponens is complete for first-order logic with only Horn clauses.
Resolution rule By noting $f_1, ..., f_n$, $g_1, ..., g_m$, $p$, $q$ formulas and by calling $theta=textrm{Unify}(p,q)$, the first-order logic version of the resolution rule can be written:
Semi-decidability First-order logic, even restricted to only Horn clauses, is semi-decidable.
- if $textrm{KB}models f$, forward inference on complete inference rules will prove $f$ in finite time
- if $textrm{KB}notmodels f$, no algorithm can show this in finite time
A digital logic gate is a discrete control circuit which takes the boolean signal at its input and outputs a Boolean signal that is based on some rules.
Contents
AND Gate
The AND gate is equivalent to two series connected switches that energize a lamp.
Logic Gate Cheat Sheet
One can simply consider the AND operation as multiplication of inputs.
OR Gate
OR gate can be considered as the two parallel connected switches energizing a lamp.
All other logic gates are a simple combination of these logic gates.
NAND and NOR Gate

Compared to other logic gates the NAND and NOR gates are easier to fabricate. The NAND gate is known as the universal gate since all other logic can be developed from it.
